Skip to contents

3. Priors

Source: vignettes/vig3_priors.Rmd
vig3_priors.Rmd

1 Set-up 

suppressPackageStartupMessages({
  library(bage)
  library(poputils)
  library(ggplot2)
  library(dplyr)
})  
#> Error in get(paste0(generic, ".", class), envir = get_method_env()) : 
#>   object 'type_sum.accel' not found
plot_exch <- function(draws) {
  ggplot(draws, aes(x = element, y = value)) +
    facet_wrap(vars(draw), nrow = 1) +
    geom_hline(yintercept = 0, col = "grey") +
    geom_point(col = "darkblue", size = 0.7) +
    scale_x_continuous(n.breaks = max(draws$element)) +
    xlab("Unit") +
    ylab("") +
    theme(text = element_text(size = 8))
}          
plot_cor_one <- function(draws) {
  ggplot(draws, aes(x = along, y = value)) +
    facet_wrap(vars(draw), nrow = 1) +
    geom_hline(yintercept = 0, col = "grey") +
    geom_line(col = "darkblue") +
    xlab("Unit") +
    ylab("") +
    theme(text = element_text(size = 8))
}          
plot_cor_many <- function(draws) {
  ggplot(draws, aes(x = along, y = value)) +
    facet_grid(vars(by), vars(draw)) +
    geom_hline(yintercept = 0, col = "grey") +
    geom_line(col = "darkblue") +
    xlab("Unit") +
    ylab("") +
    theme(text = element_text(size = 8))
}          
plot_svd_one <- function(draws) {
  ggplot(draws, aes(x = age_mid(age), y = value, color = sexgender)) +
    facet_wrap(vars(draw), nrow = 1) +
    geom_line() +
    scale_color_manual(values = c("darkgreen", "darkorange")) +
    xlab("Age") +
    ylab("") +
    theme(text = element_text(size = 8),
          legend.position = "top",
          legend.title = element_blank())
}
plot_svd_many <- function(draws) {
  draws |>
    mutate(element = paste("Unit", element)) |>
    ggplot(aes(x = age_mid(age), y = value, color = sexgender)) +
    facet_grid(vars(element), vars(draw)) +
    geom_line() +
    scale_color_manual(values = c("darkgreen", "darkorange")) +
    xlab("Age") +
    ylab("") +
    theme(text = element_text(size = 8),
          legend.position = "top",
          legend.title = element_blank())
}

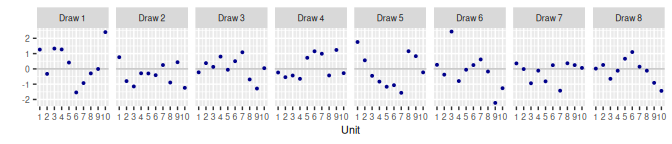
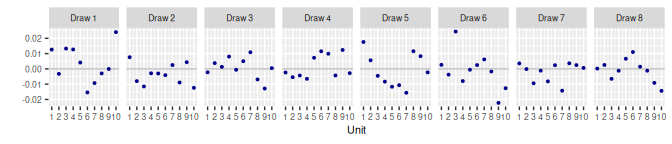
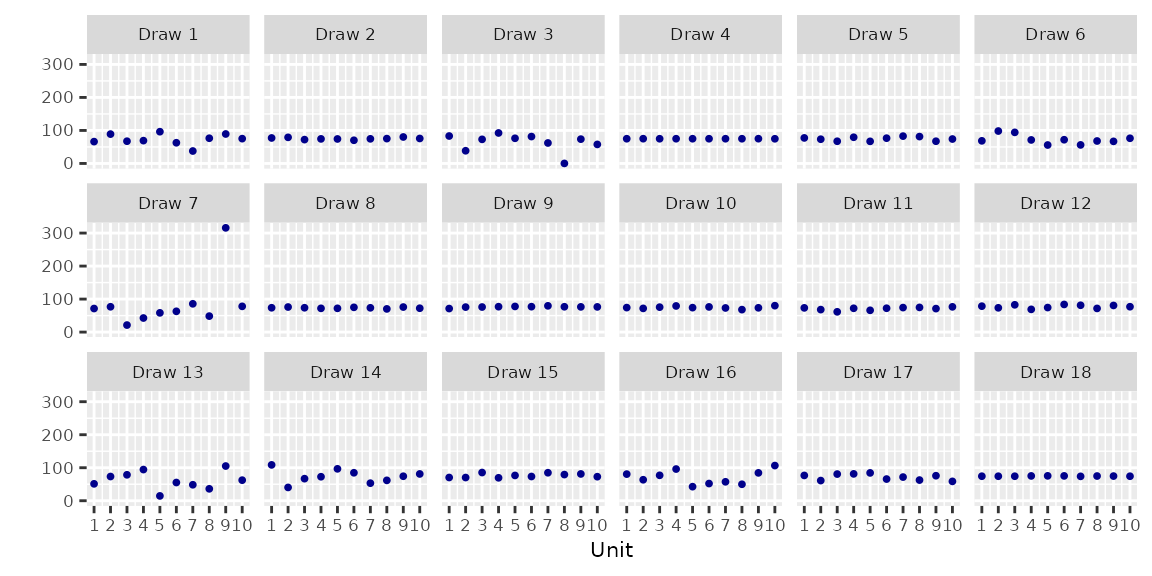
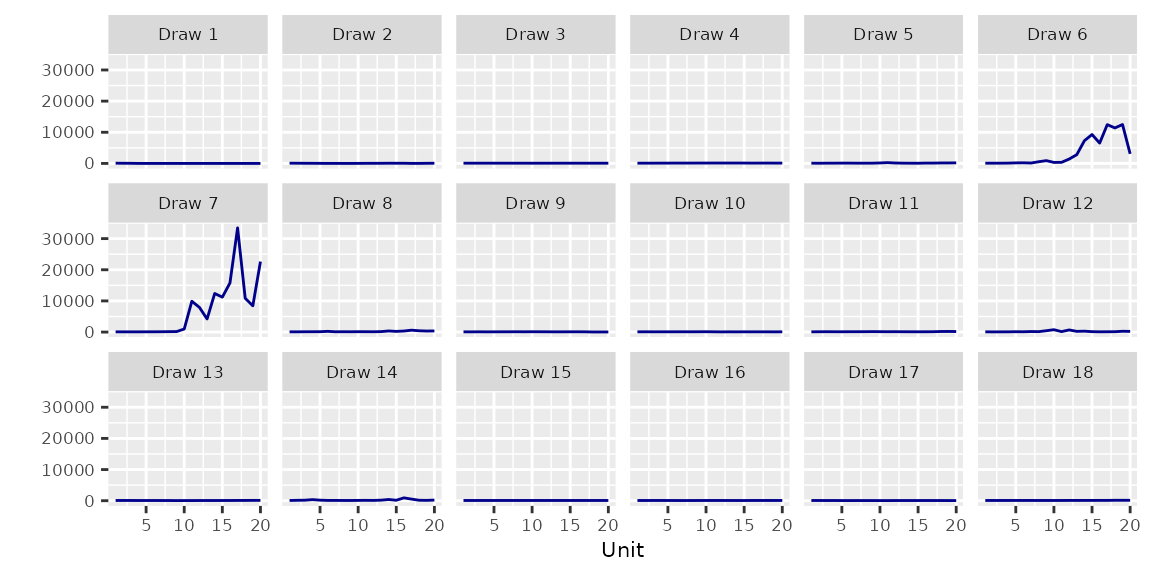
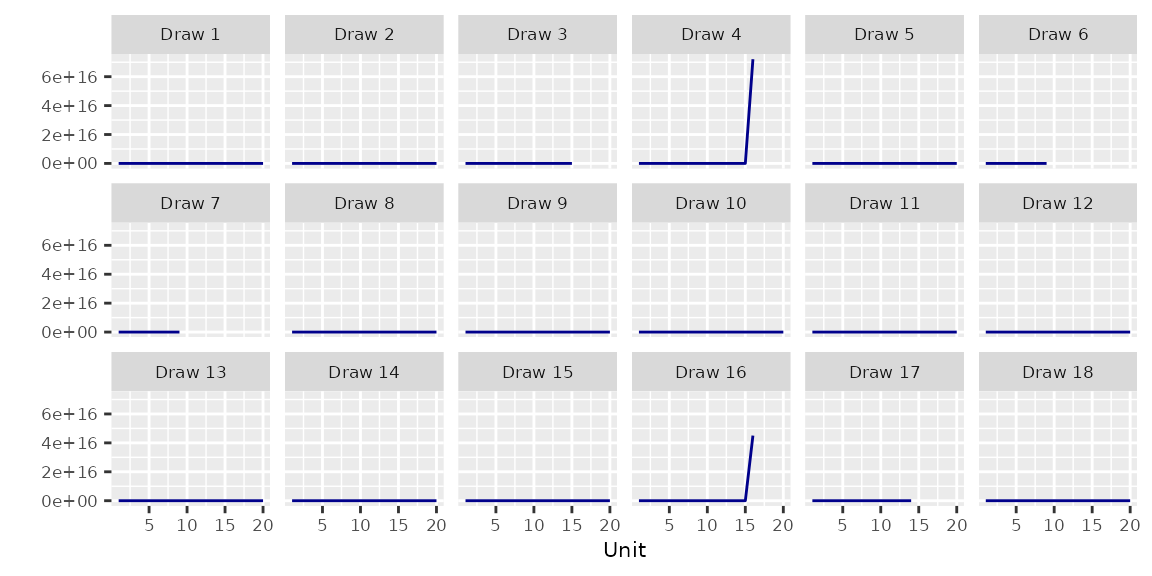
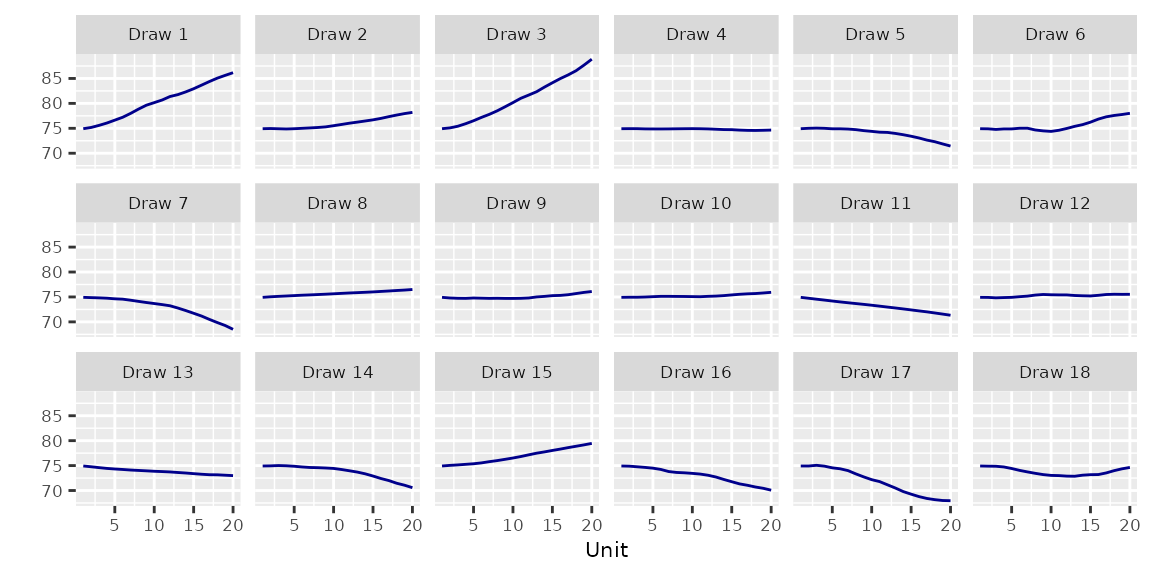
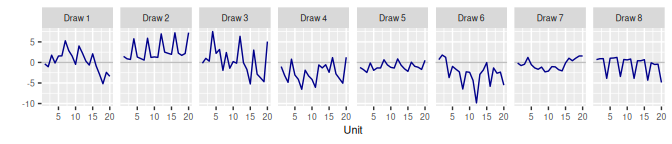
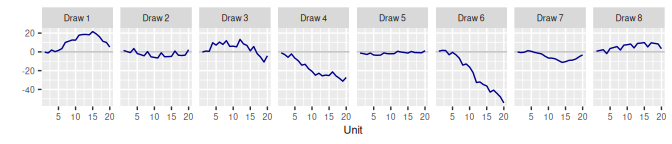
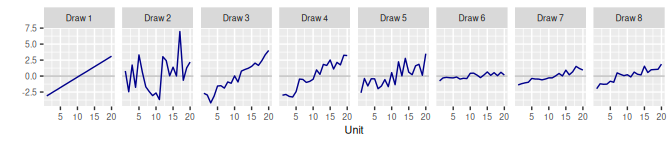
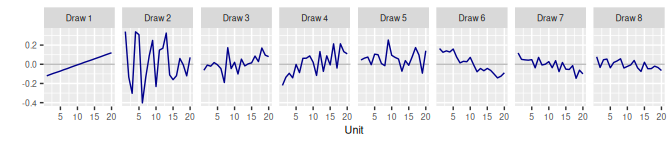
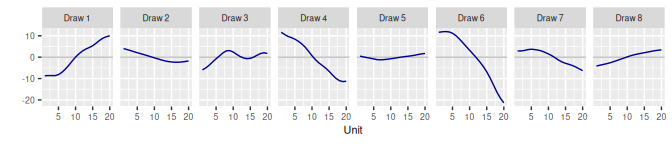
2 Exchangeable Units

2.1 Fixed Normal NFix()

2.1.1 Model

\[\begin{equation} \beta_j \sim \text{N}(0, \mathtt{sd}^2) \end{equation}\]

2.1.2 All defaults

sd = 1

set.seed(0)

NFix() |>
  generate(n_element = 10, n_draw = 8) |>
  plot_exch()

2.1.3 Reduce sd

sd = 0.01

set.seed(0)

NFix(sd = 0.01) |>
  generate(n_element = 10, n_draw = 8) |>
  plot_exch()

2.2 Normal N()

2.2.1 Model

\[\begin{align} \beta_j & \sim \text{N}(0, \tau^2) \\ \tau & \sim \text{N}^+(0, \mathtt{s}) \end{align}\]

2.2.2 All defaults

s = 1

set.seed(0)

N() |>
  generate(n_element = 10, n_draw = 8) |>
  plot_exch()

2.2.3 Reduce s

s = 0.01

set.seed(0)

N(s = 0.01) |>
  generate(n_element = 10, n_draw = 8) |>
  plot_exch()

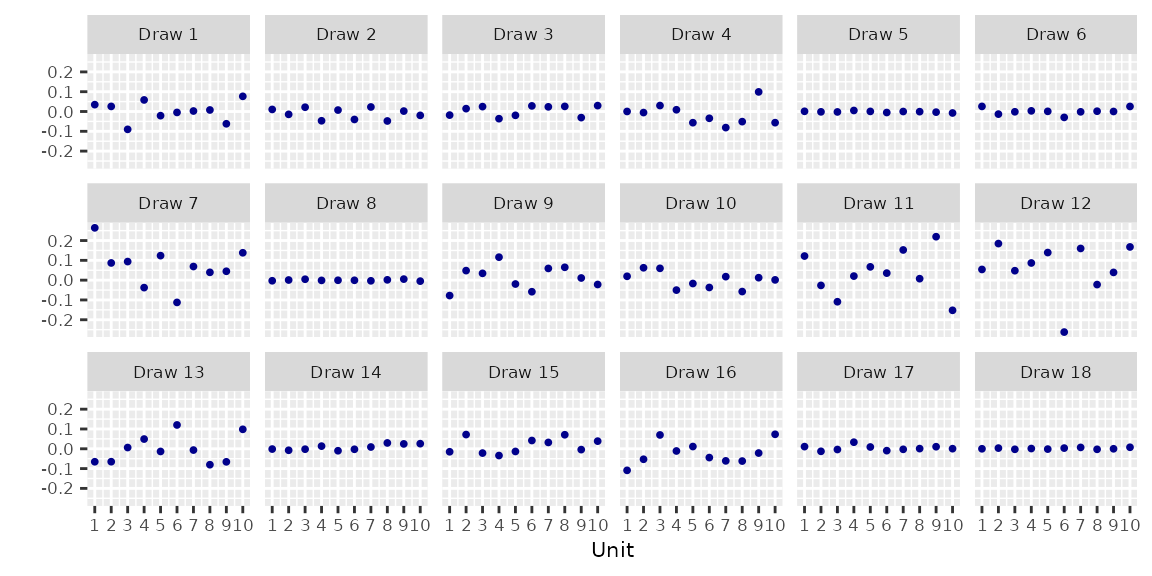
3 Units Correlated With Neighbours

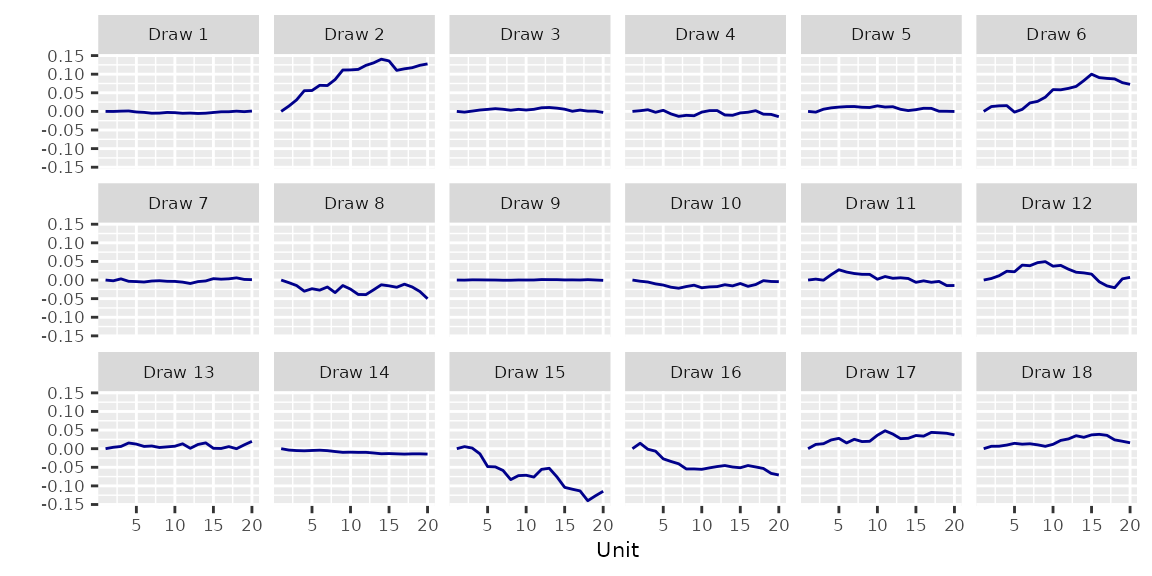
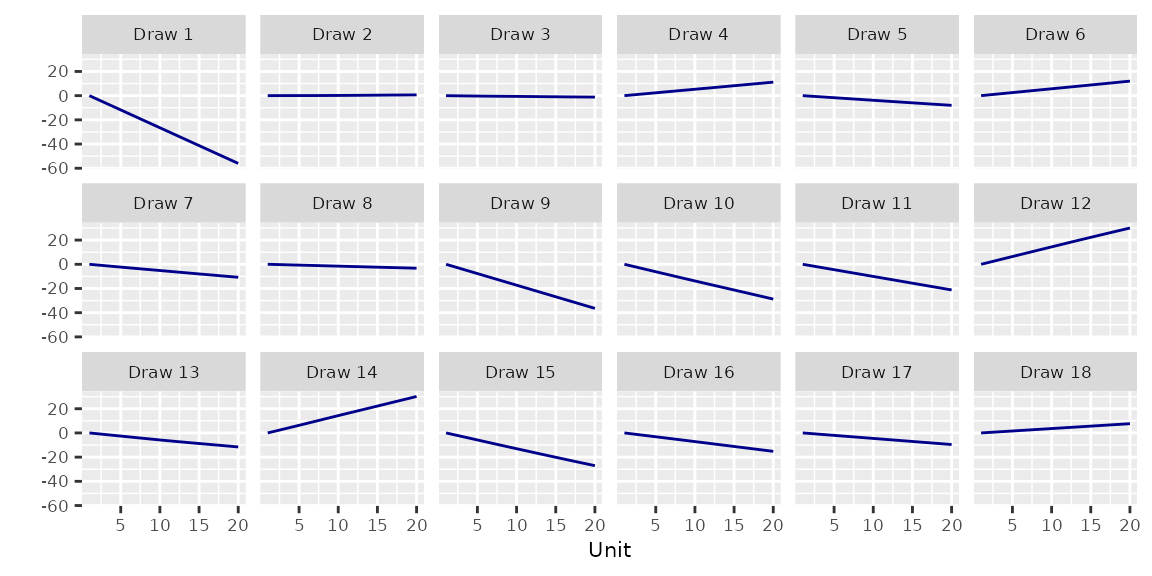
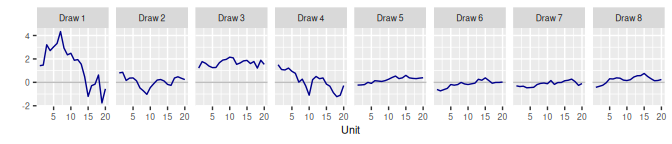
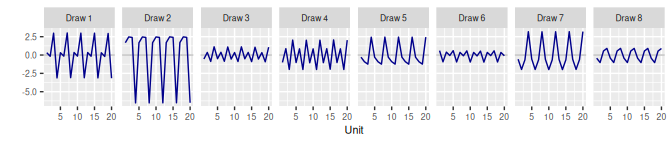
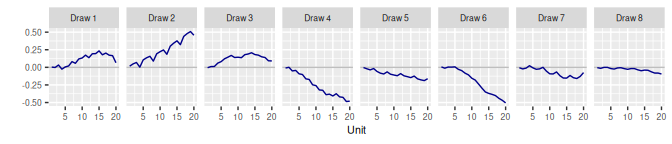
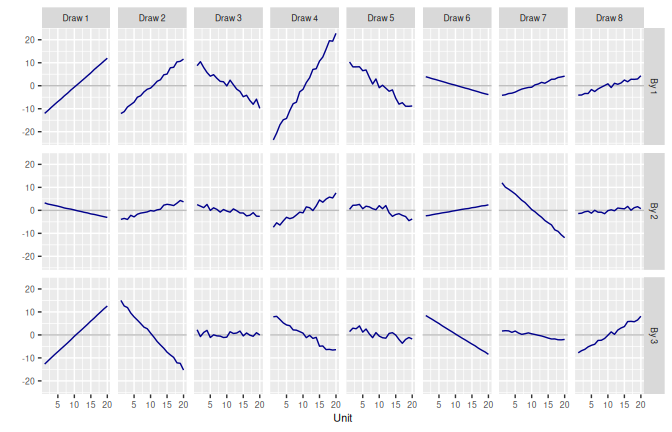
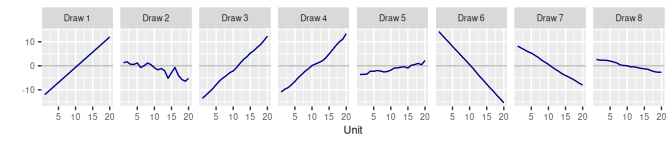
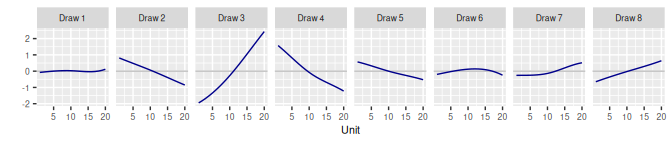
3.1 Random Walk RW()

3.1.1 Model

\[\begin{align} \beta_1 & \sim \text{N}(0, \mathtt{sd}^2) \\ \beta_j & \sim \text{N}(\beta_{j-1}, \tau^2), \quad j = 2, \cdots, J \\ \tau & \sim \text{N}^+(0, \mathtt{s}^2) \end{align}\]

3.1.2 All defaults

s = 1, sd = 1

set.seed(0)

RW() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.1.3 Reduce s

s = 0.01, sd = 1

set.seed(0)

RW(s = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.1.4 Reduce s and sd

s = 0.01, sd = 0

set.seed(0)

RW(s = 0.01, sd = 0) |>
  generate(n_draw = 8) |>
  plot_cor_one()

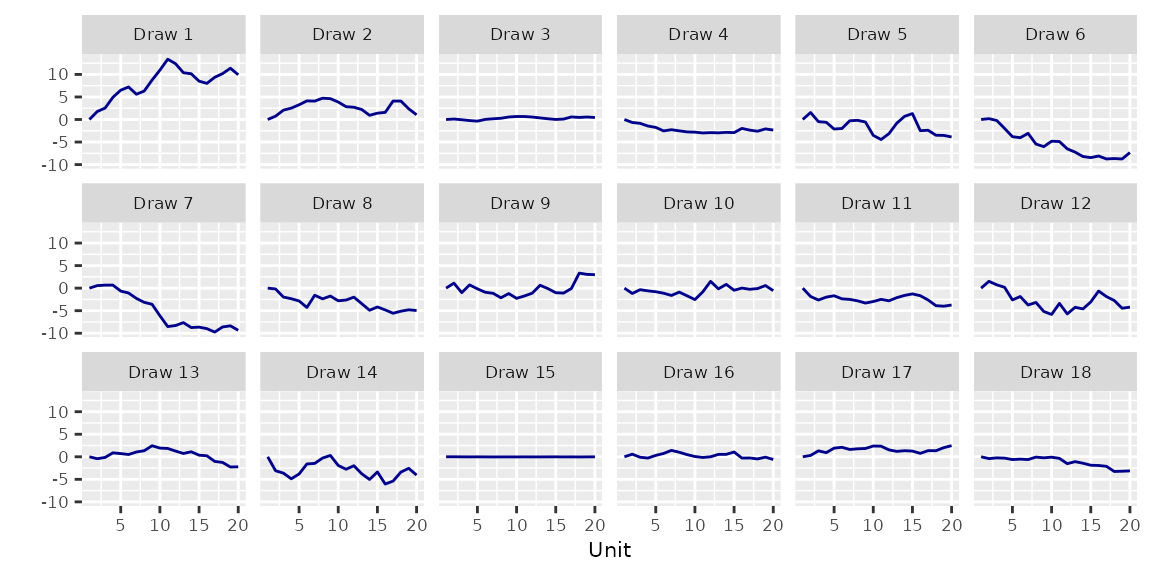
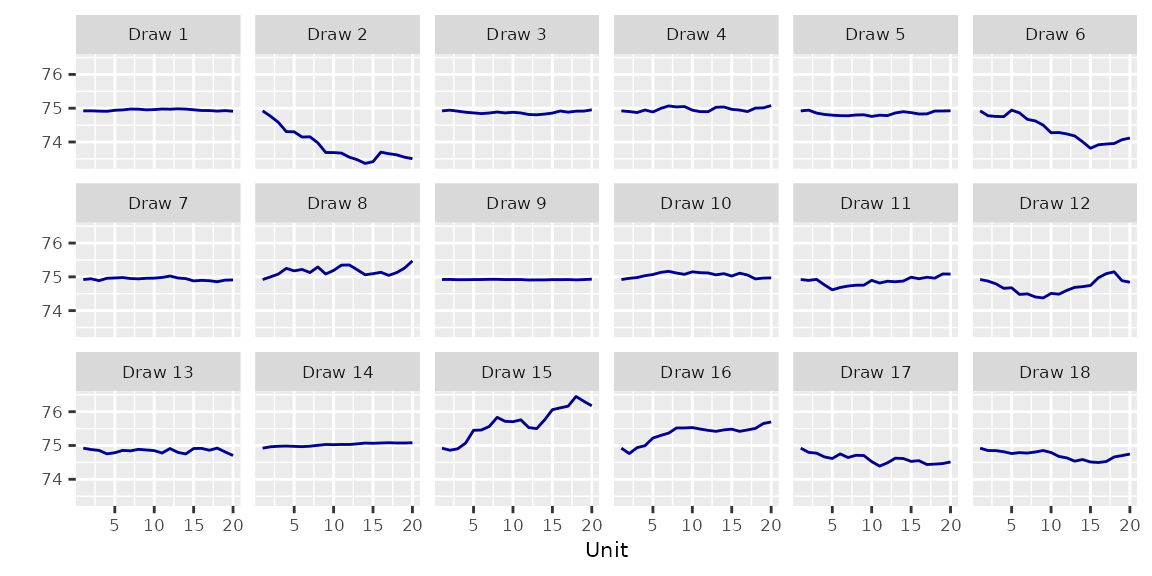
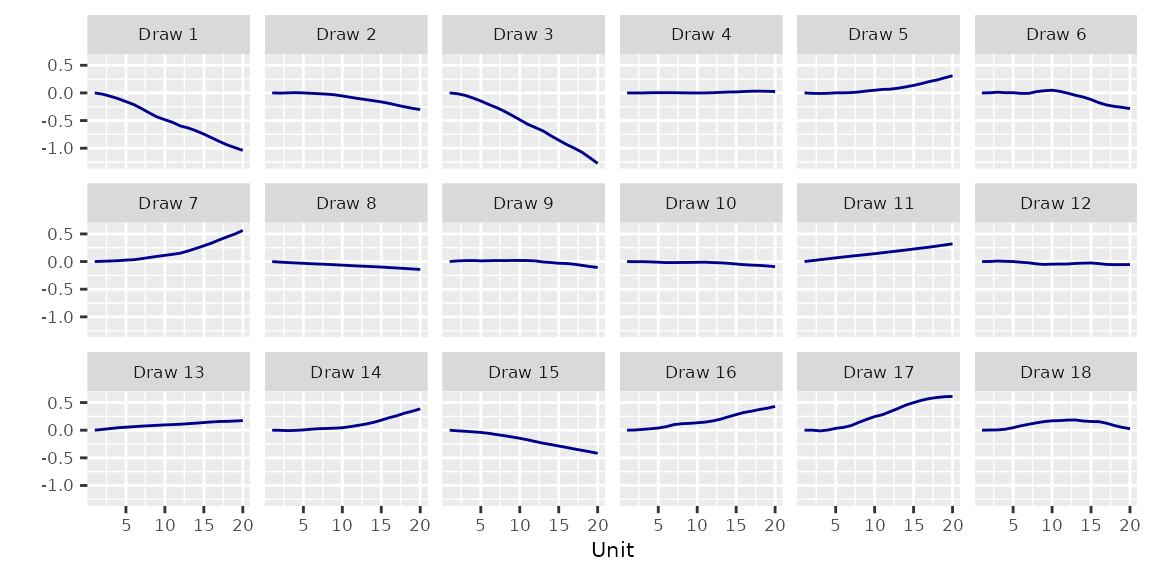
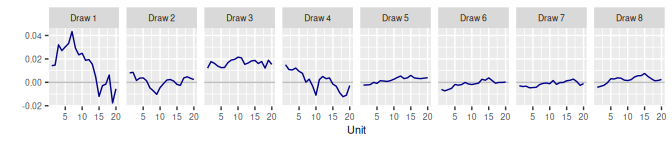
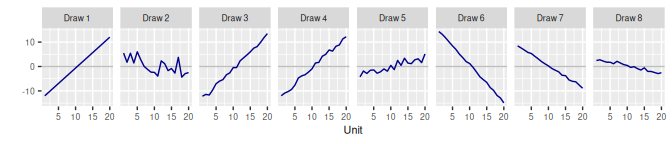
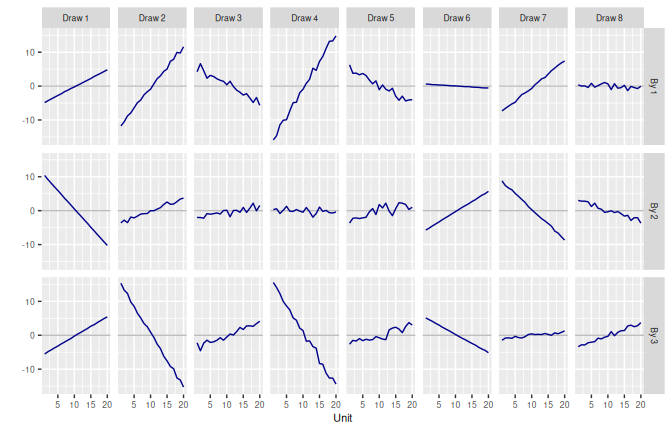
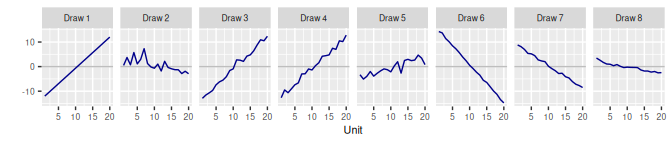
3.2 Second-Order Random Walk RW2()

3.2.1 Model

\[\begin{align} \beta_1 & \sim \text{N}(0, \mathtt{sd}^2) \\ \beta_2 & \sim \text{N}(\beta_1, \mathtt{sd\_slope}^2) \\ \beta_j & \sim \text{N}(2\beta_{j-1} - \beta_{j-2}, \tau^2), \quad j = 3, \cdots, J \\ \tau & \sim \text{N}^+(0, \mathtt{s}^2) \end{align}\]

3.2.2 All defaults

s = 1, sd = 1, sd_slope = 1

set.seed(0)

RW2() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.2.3 Reduce s

s = 0.01, sd = 1, sd_slope = 1

set.seed(0)

RW2(s = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.2.4 Reduce s and sd_slope

s = 0.01, sd = 1, sd_slope = 0.01

set.seed(0)

RW2(s = 0.01, sd_slope = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.2.5 Reduce s, sd, and sd_slope

s = 0.01, sd = 0, sd_slope = 0.01

set.seed(0)

RW2(s = 0.01, sd = 0, sd_slope = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

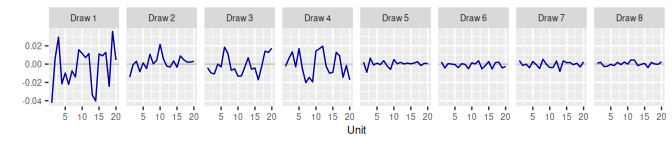
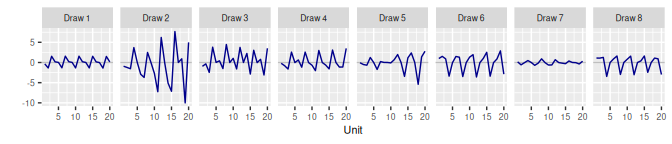
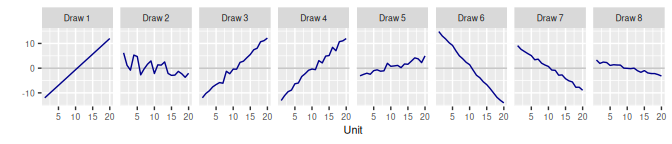
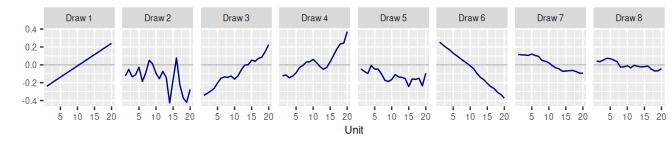
3.3 Autoregressive AR()

3.3.1 Model

\[\begin{equation} \beta_j \sim \text{N}\left(\phi_1 \beta_{j-1} + \cdots + \phi_{\mathtt{n\_coef}} \beta_{j-\mathtt{n\_coef}}, \omega^2\right) \end{equation}\] TMB derives a value of \(\omega\) that gives each \(\beta_j\) variance \(\tau^2\). The prior for \(\tau\) is \[\begin{equation} \tau \sim \text{N}^+(0, \mathtt{s}^2). \end{equation}\] The prior for each \(\phi_k\) is \[\begin{equation} \frac{\phi_k + 1}{2} \sim \text{Beta}(\mathtt{shape1}, \mathtt{shape2}). \end{equation}\]

3.3.2 All defaults

n_coef = 2, s = 1

set.seed(0)

AR() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.3.3 Increase n_coef 

set.seed(0)

AR(n_coef = 3) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.3.4 Reduce s 

set.seed(0)

AR(s = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.3.5 Specify ‘along’ and ‘by’ dimensions 

set.seed(0)

AR() |>
  generate(n_along = 20, n_by = 3, n_draw = 8) |>
  plot_cor_many()

3.3.6 Specify ‘along’ and ‘by’ dimensions, set con = "by" 

set.seed(0)

AR(con = "by") |>
  generate(n_along = 20, n_by = 3, n_draw = 8) |>
  plot_cor_many()

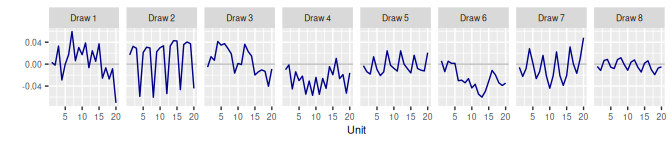
3.4 First-Order Autoregressive AR1()

3.4.1 Model

\[\begin{equation} \beta_j \sim \text{N}\left(\phi \beta_{j-1}, \omega^2\right) \end{equation}\] TMB derives a value of \(\omega\) that gives each \(\beta_j\) variance \(\tau^2\). The prior for \(\tau\) is \[\begin{equation} \tau \sim \text{N}^+(0, \mathtt{s}^2). \end{equation}\] The prior for \(\phi\) is \[\begin{equation} \frac{\phi - \mathtt{min}}{\mathtt{max} - \mathtt{min}} \sim \text{Beta}(\mathtt{shape1}, \mathtt{shape2}). \end{equation}\]

3.4.2 All defaults

s = 1, min = 0.8, max = 0.98

set.seed(0)

AR1() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.4.3 Reduce s 

set.seed(0)

AR1(s = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.4.4 Reduce s and modify min, max 

set.seed(0)

AR1(s = 0.01, min = -1, max = 1) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.5 Random Walk with Seasonal Effects RW_Seas()

3.5.1 Model

\[\begin{align} \beta_j & = \alpha_j + \lambda_j \\ \alpha_1 & \sim \text{N}(0, \mathtt{sd}^2) \\ \alpha_j & \sim \text{N}(\alpha_{j-1}, \tau^2), \quad j = 2, \cdots, J \\ \tau & \sim \text{N}^+\left(0, \mathtt{s}^2\right) \\ \lambda_j & \sim \text{N}(0, \mathtt{sd\_seas}^2), \quad j = 1, \cdots, \mathtt{n\_seas} - 1 \\ \lambda_j & = -\sum_{s=1}^{j-1} \lambda_{j-s}, \quad j = \mathtt{n\_seas},\; 2 \mathtt{n\_seas}, \cdots \\ \lambda_j & \sim \text{N}(\lambda_{j-\mathtt{n\_seas}}, \omega^2), \quad \text{otherwise} \\ \omega & \sim \text{N}^+\left(0, \mathtt{s\_seas}^2\right) \end{align}\]

3.5.2 All defaults

s = 1, sd = 1, s_seas = 0, sd_seas = 1

set.seed(0)

RW_Seas(n_seas = 4) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.5.3 Reduce s, sd

s = 0.01, sd = 0, s_seas = 0, sd_seas = 1

set.seed(0)

RW_Seas(n_seas = 4, s = 0.01, sd = 0) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.5.4 Increase s_seas

s = 0.01, sd = 0, s_seas = 1, sd_seas = 1

set.seed(0)

RW_Seas(n_seas = 4, s = 0.01, sd = 0, s_seas = 1) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.5.5 Reduce sd_seas

s = 0.01, sd = 0, s_seas = 1, s_seas = 0, sd_seas = 0.01

set.seed(0)

RW_Seas(n_seas = 4, s = 0.01, sd = 0, sd_seas = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.6 Second-Order Random Walk with Seasonal Effects RW2_Seas()

3.6.1 Model

\[\begin{align} \beta_j & = \alpha_j + \lambda_j \\ \alpha_1 & \sim \text{N}(0, \mathtt{sd}^2) \\ \alpha_2 & \sim \text{N}(\alpha_1, \mathtt{sd\_slope}^2) \\ \alpha_j & \sim \text{N}(2\alpha_{j-1} - \alpha_{j-2}, \tau^2), \quad j = 3, \cdots, J \\ \tau & \sim \text{N}^+\left(0, \mathtt{s}^2\right) \\ \lambda_j & \sim \text{N}(0, \mathtt{sd\_seas}^2), \quad j = 1, \cdots, \mathtt{n\_seas} - 1 \\ \lambda_j & = -\sum_{s=1}^{j-1} \lambda_{j-s}, \quad j = \mathtt{n\_seas},\; 2 \mathtt{n\_seas}, \cdots \\ \lambda_j & \sim \text{N}(\lambda_{j-\mathtt{n\_seas}}, \omega^2), \quad \text{otherwise} \\ \omega & \sim \text{N}^+\left(0, \mathtt{s\_seas}^2\right) \end{align}\]

3.6.2 All defaults

s = 1, sd = 1, sd_slope = 1, s_seas = 0, sd_seas = 1

set.seed(0)

RW2_Seas(n_seas = 4) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.6.3 Reduce s, sd, sd_slope, sd_seas

s = 0.01, sd = 0, sd_slope = 0.01, s_seas = 0, sd_seas = 0.01

set.seed(0)

RW2_Seas(n_seas = 4, s = 0.01, sd = 0, sd_slope = 0.01, sd_seas = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

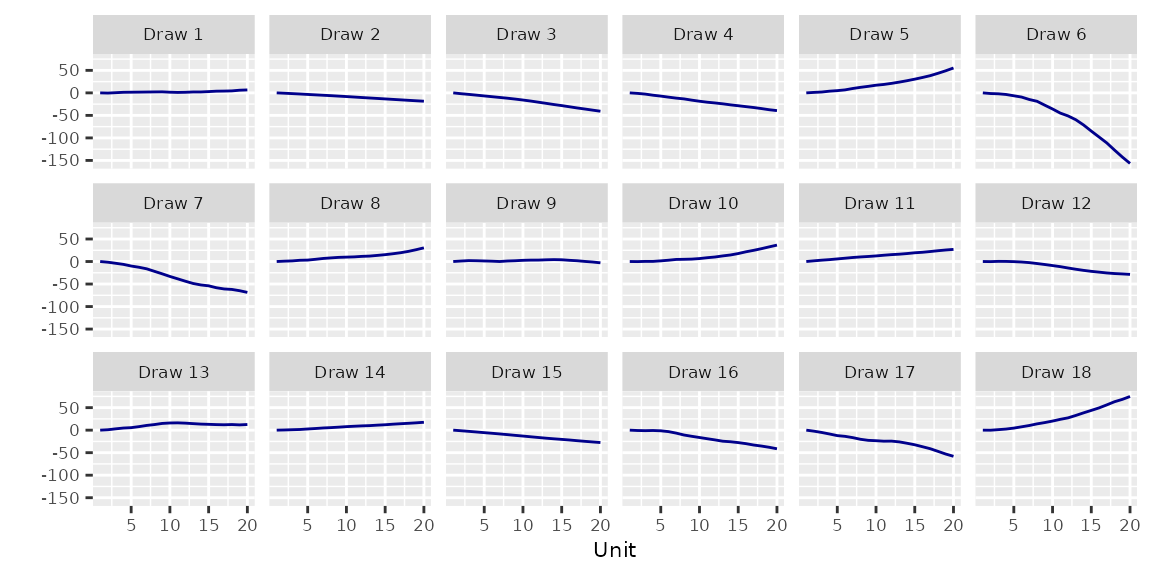
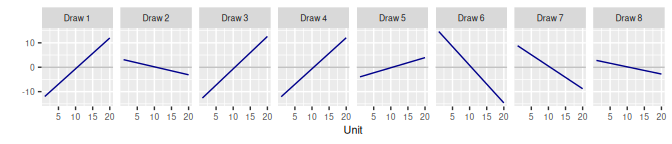
3.7 Linear Lin()

3.7.1 Model

\[\begin{align} \beta_j & = \alpha_j + \epsilon_j \\ \alpha_j & = \left(j - \frac{J + 1}{2}\right) \eta \\ \eta & \sim \text{N}\left(\mathtt{mean\_slope}, \mathtt{sd\_slope}^2 \right) \\ \epsilon & \sim \text{N}(0, \tau^2) \\ \tau & \sim \text{N}^+\left(0, \mathtt{s}^2\right) \end{align}\]

3.7.2 All defaults

s = 1, mean_slope = 0, sd_slope = 1

set.seed(0)

Lin() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.7.3 Reduce s

s = 0, mean_slope = 0, sd_slope = 1

set.seed(0)

Lin(s = 0) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.7.4 Modify mean_slope, sd_slope

s = 1, mean_slope = 0.2, sd_slope = 0.1

set.seed(0)

Lin(mean_slope = 0.2, sd_slope = 0.1) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.7.5 Specify ‘along’ and ‘by’ dimensions 

set.seed(0)

Lin() |>
  generate(n_along = 20, n_by = 3, n_draw = 8) |>
  plot_cor_many()

3.7.6 Specify ‘along’ and ‘by’ dimensions, set con = "by" 

set.seed(0)

Lin(con = "by") |>
  generate(n_along = 20, n_by = 3, n_draw = 8) |>
  plot_cor_many()

3.8 Linear with AR Errors Lin_AR()

3.8.1 Model

\[\begin{align} \beta_j & = \alpha_j + \epsilon_j \\ \alpha_j & = \left(j - \frac{J + 1}{2}\right) \eta \\ \eta & \sim \text{N}\left(\mathtt{mean\_slope}, \mathtt{sd\_slope}^2 \right) \\ \epsilon_j & \sim \text{N}\left(\phi_1 \epsilon_{j-1} + \cdots + \phi_{\mathtt{n\_coef}} \epsilon_{j-\mathtt{n\_coef}}, \omega^2\right) \tau & \sim \text{N}^+\left(0, \mathtt{s}^2\right) \\ \frac{\phi_k + 1}{2} & \sim \text{Beta}(\mathtt{shape1}, \mathtt{shape2}) \end{align}\]

3.8.2 All defaults

n_coef = 2, s = 1, mean_slope = 0, sd_slope = 1

set.seed(0)

Lin_AR() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.8.3 Reduce s, sd_slope

s = 0.1, mean_slope = 0, sd_slope = 0.01

set.seed(0)

Lin_AR(s = 0.1, sd_slope = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.9 Linear with AR1 Errors Lin_AR1()

3.9.1 Model

\[\begin{align} \beta_j & = \alpha_j + \epsilon_j \\ \alpha_j & = \left(j - \frac{J + 1}{2}\right) \eta \\ \eta & \sim \text{N}\left(\mathtt{mean\_slope}, \mathtt{sd\_slope}^2 \right) \\ \epsilon_j & \sim \text{N}\left(\phi \epsilon_{j-1}, \omega^2\right) \tau & \sim \text{N}^+\left(0, \mathtt{s}^2\right) \\ \frac{\phi - \mathtt{min}}{\mathtt{max} - \mathtt{min}} \sim \text{Beta}(\mathtt{shape1}, \mathtt{shape2}) \end{align}\]

3.9.2 All defaults

s = 1, min = 0.8, max = 0.98, mean_slope = 0, sd_slope = 1

set.seed(0)

Lin_AR1() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.9.3 Modify min, max

s = 1, min = -1, max = 1, mean_slope = 0, sd_slope = 1

set.seed(0)

Lin_AR1(min = -1, max = 1) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.9.4 Reduce s, sd_slope

s = 0.1, min = 0.8, max = 0.98, mean_slope = 0, sd_slope = 0.02

set.seed(0)

Lin_AR1(s = 0.1, sd_slope = 0.02) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.10 Penalised Spline Sp()

3.10.1 Model

\[\begin{align} \pmb{\beta} & = \bm{X} \pmb{\alpha} \\ \alpha_1 & \sim \text{N}(0, \mathtt{sd}^2) \\ \alpha_2 & \sim \text{N}(\alpha_1, \mathtt{sd\_slope}^2) \\ \alpha_j & \sim \text{N}(2\alpha_{j-1} - \alpha_{j-2}, \tau^2), \quad j = 3, \cdots, J \\ \tau & \sim \text{N}^+\left(0, \mathtt{s}^2\right) \\ \end{align}\]

3.10.2 All defaults

n_comp = NULL, s = 1, sd = 1, sd_slope = 1

set.seed(0)

Sp() |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.10.3 Specify n_comp

n_comp = 15, s = 1, sd = 1, sd_slope = 1

set.seed(0)

Sp(n_comp = 5) |>
  generate(n_draw = 8) |>
  plot_cor_one()

3.10.4 Reduce s, sd, sd_slope

n_comp = NULL, s = 0.01, sd = 0.01, sd_slope = 0.01

set.seed(0)

Sp(s = 0.01, sd = 0.01, sd_slope = 0.01) |>
  generate(n_draw = 8) |>
  plot_cor_one()

4 SVD-Based Priors

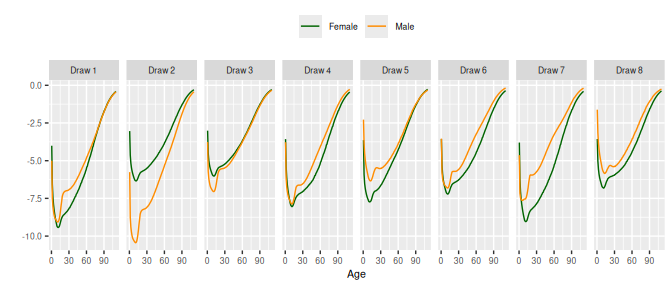
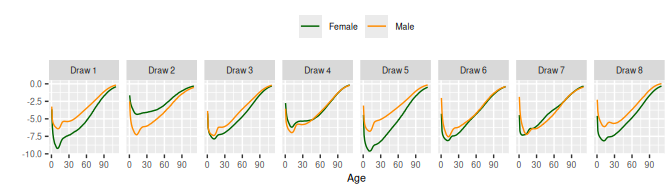
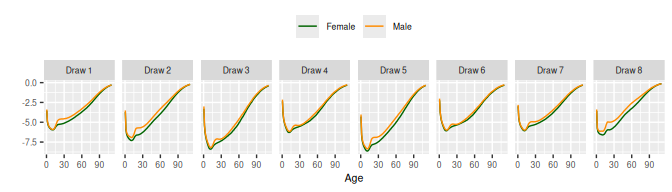
4.1 Exchangeable SVD()

4.1.1 Model

\[\begin{equation} \pmb{\beta} = \pmb{F} \pmb{\alpha} + \pmb{g} \end{equation}\]

4.1.2 All defaults

n_comp = NULL, indep = TRUE

set.seed(0)

SVD(HMD) |>
  generate(n_draw = 8) |>
  plot_svd_one()

4.1.3 Increase n_comp

n_comp = 5, indep = TRUE

SVD(HMD, n_comp = 5) |>
  generate(n_draw = 8) |>
  plot_svd_one()

4.1.4 Set indep to FALSE 

SVD(HMD, indep = FALSE) |>
  generate(n_draw = 8) |>
  plot_svd_one()

4.1.5 Multiple units 

SVD(HMD, indep = FALSE) |>
  generate(n_draw = 8, n_element = 3) |>
  plot_svd_many()

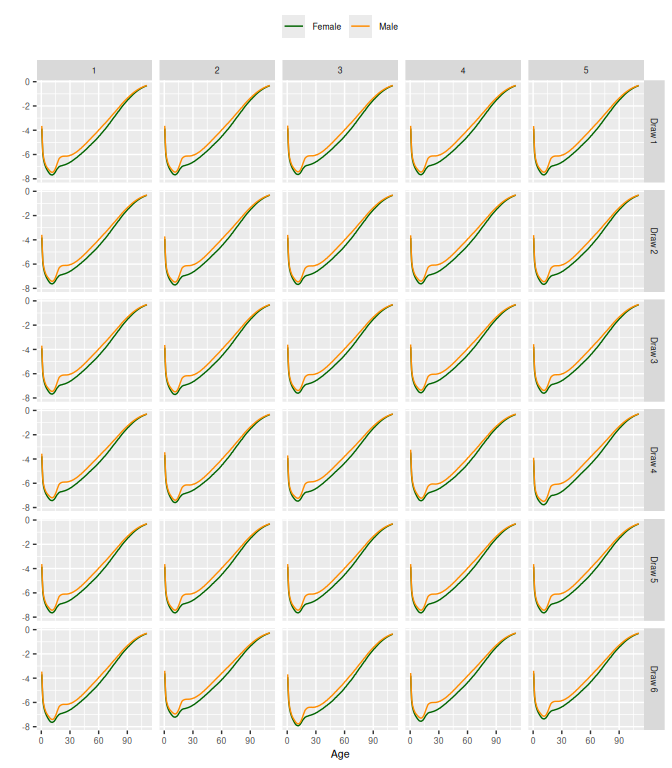
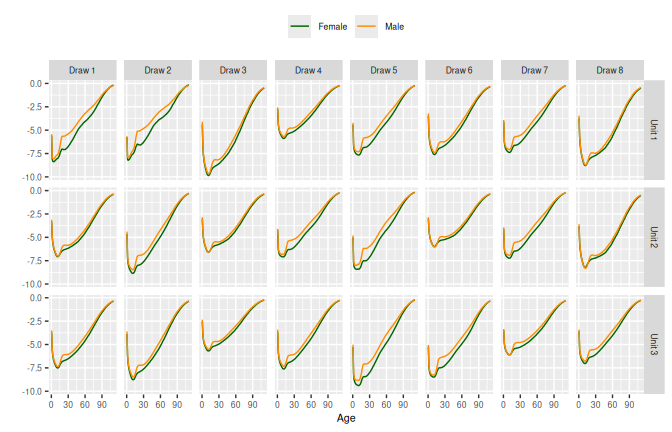
4.2 Dynamic SVD Prior: SVD_AR() 

SVD_AR(HMD, indep = FALSE, s = 0.1) |>
  generate(n_draw = 6, n_along = 5) |>
    ggplot(aes(x = age_mid(age), 
                      y = value, 
                      color = sexgender)) +
      facet_grid(vars(draw), vars(along)) +
      geom_line() +
      scale_color_manual(values = c("darkgreen", "darkorange")) +
      xlab("Age") +
      ylab("") +
      theme(text = element_text(size = 8),
            legend.position = "top",
            legend.title = element_blank())