1 Introduction
Simulation studies can be used to assess the performance of a model. The basic idea is to generate some parameter values, use these parameters to generate some data, use the data to try to infer the original parameter values, and then see how close the inferred parameter values are to the actual parameter values.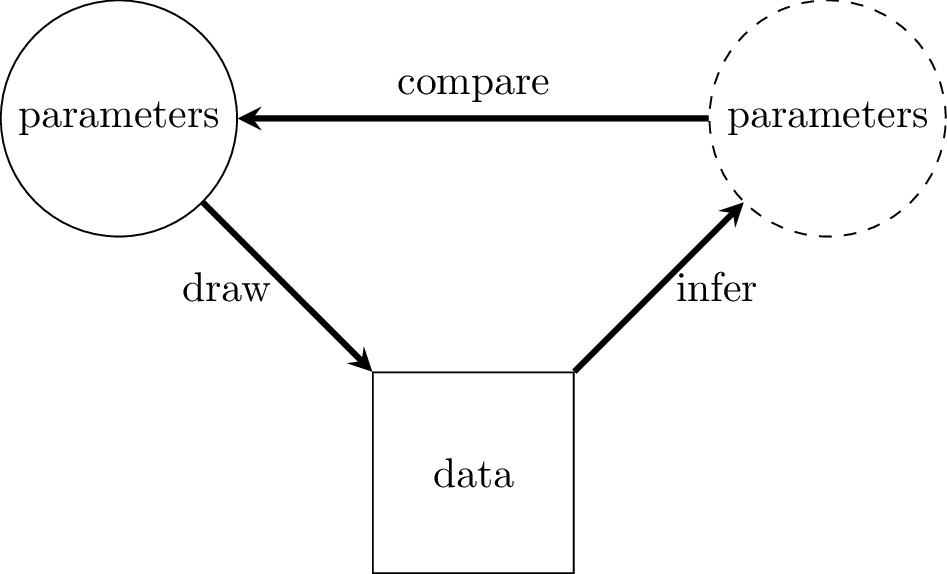
Figure 1.1: Simulation study of a model
Function report_sim() automates the process of doing a simulation study. We are still experimenting with report_sim(), and the interface may change. Suggestions are welcome, ideally through raising an issue here.
2 Estimation model matches data generation model
The most straightforward type of simulation is when the estimation model' used to do the inference matches thedata generation model’ used to create the data. Even when the estimation model matches the data generation model, the inferred values for the parameters will not exactly reproduce the actual values, since data is drawn at random, and provides a noisy signal about parameters it was generated from. However, if the experiment is repeated many times, with a different randomly-drawn dataset each time, the errors should more or less average out at zero, 50% credible intervals should contain the true values close to 50% of the time, and 95% credible intervals should contain the true values close to 95% of the time.
To illustrate, we use investigate the performance of a model of divorce rates in New Zealand. We reduce the number of ages and time periods to speed up the calculations.
library(bage)
#> Loading required package: rvec
#>
#> Attaching package: 'rvec'
#> The following objects are masked from 'package:stats':
#>
#> sd, var
#> The following object is masked from 'package:base':
#>
#> rank
library(dplyr, warn.conflicts = FALSE)
library(poputils)
divorces_small <- nzl_divorces |>
filter(age_upper(age) < 40,
time >= 2016) |>
droplevels()
mod <- mod_pois(divorces ~ age * sex + time,
data = divorces_small,
exposure = population)
mod
#>
#> ------ Unfitted Poisson model ------
#>
#>
#> divorces ~ age * sex + time
#>
#> exposure = population
#>
#>
#> term prior along n_par n_par_free
#> (Intercept) NFix() - 1 1
#> age RW() age 4 3
#> sex NFix() - 2 2
#> time RW() time 6 5
#> age:sex RW() age 8 6
#>
#>
#> n_draw pr_mean_disp var_time var_age var_sexgender
#> 1000 1 time age sexTo do the simulation study, we pass the model to report_sim(). If only one model is supplied, report_sim() assumes that that model should be used as the estimation model and as the data generation model. By default report_sim() repeats the experiment 100 times, generating a different dataset each time.
set.seed(0)
res <- report_sim(mod_est = mod)
res
#> $components
#> # A tibble: 9 × 7
#> term component .error .cover_50 .cover_95 .length_50 .length_95
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) effect 0.0344 0.57 0.97 0.841 2.38
#> 2 age effect -0.0559 0.705 0.958 0.750 2.14
#> 3 age hyper 0.0947 0.38 0.81 0.593 2.07
#> 4 sex effect -0.0260 0.475 0.94 0.841 2.43
#> 5 time effect -0.0400 0.623 0.948 0.435 1.23
#> 6 time hyper 0.0211 0.55 0.95 0.384 1.26
#> 7 age:sex effect 0.0365 0.669 0.938 0.750 2.16
#> 8 age:sex hyper -0.0402 0.42 0.87 0.489 1.58
#> 9 disp disp 0.0324 0.44 0.91 0.244 0.723
#>
#> $augment
#> # A tibble: 2 × 7
#> .var .observed .error .cover_50 .cover_95 .length_50 .length_95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 .fitted 273. -0.000490 0.499 0.947 0.00739 0.0216
#> 2 .expected 273. -23.0 0.541 0.952 90.8 325.The output from report_sim() is a list of two data frames. The first data frame contains results for parameters associated with the components() function: main effects and interactions, associated hyper-parameters, and dispersion. The second data frame contains results for parameters associated with the augment() function: the lowest-level rates parameters.
As can be seen in the results, the errors do not average out at exactly zero, 50% credible intervals do not contain the true value exactly 50% of the time, and 95% credible intervals do not contain the true value exactly 95% of the time. However, increasing the number of simulations from the default value of 100 to, say, 1000 will reduce the average size of the errors closer to zero, and bring the actual coverage rates closer to their advertised values. When larger values of n_sim are used, it can be helpful to use parallel processing to speed up calculations, which is done through the n_core argument.
One slightly odd feature of the results is that the mean for .expected is very large. This reflects the fact that the data generation model draws some extreme values. We are developing a set of more informative priors that should avoid this behavior in future versions of bage.
3 Estimation model different from data generation model
In actual applications, no estimation model ever perfectly describes the true data generating process. It can therefore be helpful to see how robust a given model is to misspecification, that is, to cases where the estimation model differs from the data generation model.
With report_sim(), this can be done by using one model for the mod_est argument, and a different model for the mod_sim argument.
Consider, for instance, a case where the time effect is generated from an AR1() prior, while the estimation model continues to use the default value of a RW() prior,
mod_ar1 <- mod |>
set_prior(time ~ AR1())
mod_ar1
#>
#> ------ Unfitted Poisson model ------
#>
#>
#> divorces ~ age * sex + time
#>
#> exposure = population
#>
#>
#> term prior along n_par n_par_free
#> (Intercept) NFix() - 1 1
#> age RW() age 4 3
#> sex NFix() - 2 2
#> time AR1() time 6 6
#> age:sex RW() age 8 6
#>
#>
#> n_draw pr_mean_disp var_time var_age var_sexgender
#> 1000 1 time age sexWe set the mod_sim argument to mod_ar1 and generate the report.
res_ar1 <- report_sim(mod_est = mod, mod_sim = mod_ar1)
res_ar1
#> $components
#> # A tibble: 9 × 7
#> term component .error .cover_50 .cover_95 .length_50 .length_95
#> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) effect -0.173 0.34 0.79 0.834 2.36
#> 2 age effect -0.0472 0.67 0.95 0.716 2.04
#> 3 age hyper 0.105 0.4 0.77 0.581 2.00
#> 4 sex effect 0.0365 0.46 0.93 0.837 2.43
#> 5 time effect 0.0750 0.228 0.545 0.393 1.11
#> 6 time hyper -0.357 0.19 0.61 0.335 1.16
#> 7 age:sex effect 0.0540 0.66 0.949 0.719 2.08
#> 8 age:sex hyper -0.0521 0.43 0.88 0.466 1.51
#> 9 disp disp 0.0135 0.57 0.96 0.245 0.727
#>
#> $augment
#> # A tibble: 2 × 7
#> .var .observed .error .cover_50 .cover_95 .length_50 .length_95
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 .fitted 86.9 0.000355 0.500 0.948 0.00671 0.0195
#> 2 .expected 86.9 3.07 0.488 0.946 44.6 146.In this case, although actual coverage for the hyper-parameters (in the components part of the results) now diverges from the advertised coverage, coverage for the low-level rates (in the augment part of the results) is still close to advertised coverage.
4 The relationship between report_sim() and replicate_data()
Functions report_sim() and replicate_data() overlap, in that both use simulated data to provide insights into model performance. Their aims are, however, different. Typically, report_sim() is used before fitting a model, to assess its performance across a random selection of possible datasets, while replicate_data() is used after fitting a model, to assess its performance on the dataset to hand.